Poulpy

Overview
Poulpy is a fast, modular, and research-grade Fully Homomorphic Encryption (FHE) library written in Rust. It implements Ring-Learning-With-Errors–based homomorphic encryption over the Torus and is designed around two core principles:
- A bivariate polynomial representation of Torus polynomials
- A hardware abstraction layer (HAL) enabling backend-agnostic development
Poulpy targets both advanced research and production-oriented experimentation, with a strong emphasis on performance, modularity, and long-term maintainability.
Why Poulpy?
Poulpy departs from mainstream FHE implementations by avoiding the traditional residue number system (RNS) and instead adopting the bivariate polynomial representation proposed in
Revisiting Key Decomposition Techniques for FHE: Simpler, Faster and More Generic.
The bivariate representation used in Poulpy decouples cyclotomic arithmetic from large-integer arithmetic by decomposing coefficients in base \(2^{-K}\) over the Torus \(\mathbb{T}_N[X]\).
This provides several advantages:
- Much simpler, more generic and reusable parameterization
- Optimal bit-granular rescaling
- Unified plaintext space across schemes
- Native and efficient scheme switching
- Linear (rather than quadratic) DFT complexity in key-switching
- Simpler, deterministic, and hardware-friendly implementations
These properties make the bivariate representation particularly well suited for high-performance and hardware-accelerated FHE.
Poulpy also decouples cryptographic schemes from polynomial arithmetic through a hardware abstraction layer closely matching the API of spqlios-arithmetic, allowing applications to remain backend-agnostic and select CPU, GPU, or accelerator backends at runtime. In addition, the Poulpy team is in direct and frequent contact with the original developers of spqlios-arithmetic, ensuring close alignment with design decisions.
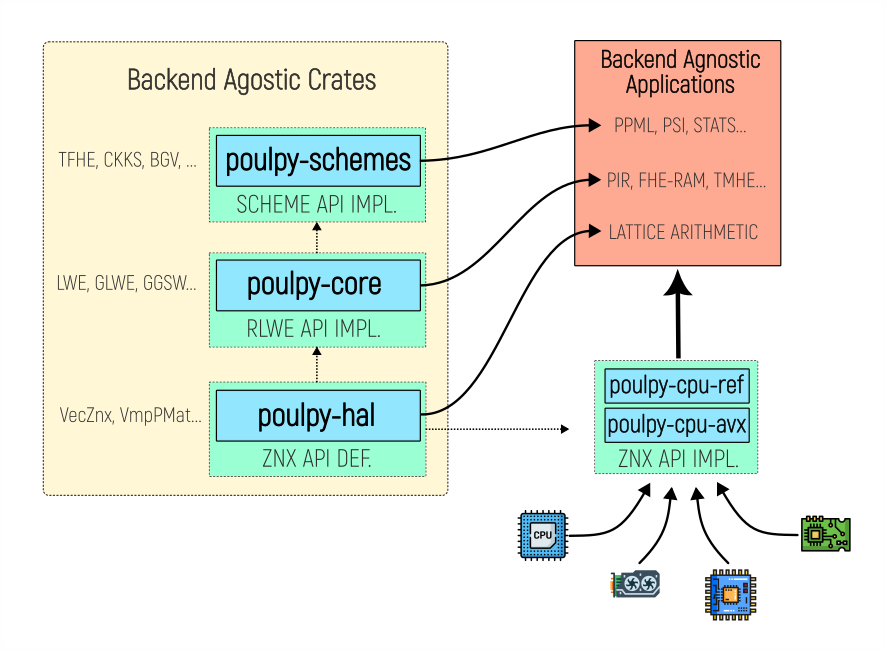
High-level architecture of Poulpy, separating cryptographic schemes, core arithmetic, and hardware backends.
License
Poulpy is a fully open-source library that is licensed under Apache 2.0.
Sustainability & Funding
Maintaining a high-quality cryptographic library requires ongoing engineering effort: design, implementation, benchmarking, optimization, documentation, and long-term architectural stewardship.
Poulpy is primarily co-developed and maintained by Ideal Rings Lab and Phantom Zone. To ensure the project’s long-term sustainability and continued development, we are seeking sponsorships to fund dedicated maintainer time.
What sponsorship supports
Sponsorship funding is used to support:
- Core library maintenance and refactoring
- Roadmap execution & documentation
- Performance optimization and benchmarking
- Additional hardware backends development
Contact: jean-philippe.bossuat@idealringslab.com
Roadmap (Indicative)
The following roadmap reflects current technical priorities and may evolve based on community and sponsor inputs.
Short term
- API stabilization of
poulpy-hal - Performance benchmarking across available backends
- Improved documentation and usage examples
Mid term
- NTT120 backend with cpu reference & AVX implementation
- SIMD schemes (CKKS/BFV/BGV)
- Threshold HE primitives
Long term
- GPU backend
- Advanced compiler and runtime integration
- Production-oriented tooling and diagnostics